
René Descartes
Né le 31 mars 1596, dans le village de la Haye, aux confins de la Touraine et du Poitou
Mort le11 février 1649
|
|
René Descartes Né le 31 mars 1596, dans le village de la Haye, aux confins de la Touraine et du Poitou Mort le11 février 1649 |
Méthode des isopérimètres
On construit par récurrence une suite de polygones réguliers P0, P1,.... ,Pn, ayant tous le même périmètre L,
Le polygone Pn ayant 2n+2 cotés.
P0 est donc le carré.
Construisons Pn+1 à partir de Pn :
Notons [An,Bn] un coté quelconque de Pn.
Soit C de centre O le cercle circonscrit à Pn et E le milieu de l'arc AnBn de C.
Soit An+1 le milieu de [An,E] et Bn+1 le milieu de [E,Bn].
On construit Pn+1 comme l'unique polygone régulier, centré en O, de coté [An+1,Bn+1]
D'après le théorème de Thalès, An+1Bn+1=AnBn/2 et donc le périmètre est inchangé.
Notons Hn le milieu de [An,Bn] et rn =OHn.
Calculons rn+1 en fonction de rn :
Comme les triangles OHn+1An+1 et An+1Hn+1E sont homothétiques ,
on a An+1Hn+1² = EHn+1 . Hn+1O.
Sachant que EHn+1 = Hn+1Hn=rn+1-rn et que An+1Hn+1=AnHn/2=A0H0/2n+1=r0/2n+1 (par récurrence ), on obtient
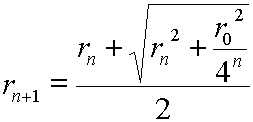
Cette suite (rn) définie par récurrence tend vers une limite r. La suite des polygones (Pn) "tend" vers un cercle de rayon r et de périmètre L=8r0 .
On a donc
p
=4 r0/r.