Archimède de Syracuse
(287 - 212 avant J.-C.), mathématicien et ingénieur grec
|
|
Archimède de Syracuse(287 - 212 avant J.-C.), mathématicien et ingénieur grec |
Méthode d'Archimède
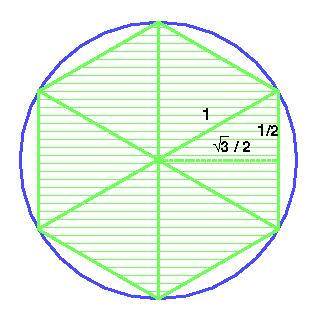
Le rayon du cercle étant 1, alors l'aire d'un triangle est :
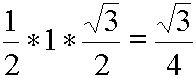
donc l'aire de l'hexagone est :
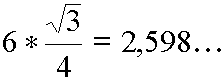
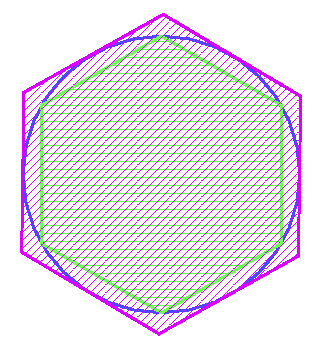
On fait un calcul analogue pour trouver l'aire du polygone circonscrit.
On trouve une valeur de : 3,464...
Donc 2,598 <
p < 3,464
Par cette méthode purement géométrique mettant en jeu les polygones réguliers à 6, 12, 24, 48, 96 côtés, Archimède démontre la double inégalité suivante: 3 + 10/71 <
p <3 + 1/7Cet encadrement donne les deux premières décimales de
p.|
Nombre de cotés |
Aire du polygone inscrit |
Aire du polygone circonscrit |
|
6 |
2, 598 076 |
3, 464 102 |
|
12 |
3, 000 000 |
3, 215 390 |
|
24 |
3, 105 829 |
3, 159 660 |
|
48 |
3, 132 629 |
3, 146 086 |
|
96 |
3, 139 350 |
3, 142 715 |
|
180 |
3, 140 955 |
3, 141 912 |
|
360 |
3, 141 433 |
3, 141 672 |
|
720 |
3, 141 553 |
3, 141 613 |
|
1440 |
3, 141 583 |
3, 141 598 |
|
2880 |
3, 141 590 |
3, 141 594 |
|
5760 |
3, 141 592 |
3, 141 593 |
Archimède s'est arrêté à ce niveau
A
la suite d'Archimède, les savants ont pendant longtemps essayé d'améliorer la méthode des polygones, et d'augmenter autant que possible le nombre de cotés. Le record en la matière appartient à Ludolph van Ceulen (16e siècle). Il consacra sa vie à ce calcul et parvint à trouver 35 décimales, à l'aide de polygones ayant 262 cotés.