
François Viète
Né en 1540 à Fontenay-le-Comte, en Vendée
Mort en 1603
|
|
François Viète Né en 1540 à Fontenay-le-Comte, en Vendée Mort en 1603 |
On prend un cercle de diamètre 2, l'aire d'un carré inscrit dans un tel cercle est de 2. L'idée consiste à construire une suite de polygones (Pn)n
³ 0, inscrits dans ce même cercle, Pn ayant 2(n+1) cotés. L'aire du polygone Pn quand n tend vers l'infini tend vers p .L'aire de P1 est égale à celle de P0 multipliée par 1/cos(
p /4)=2/Ö 2. L'aire de P2 est égale à celle de P1 multipliée par 1/cos(p /8)...Ainsi on obtient la formule :
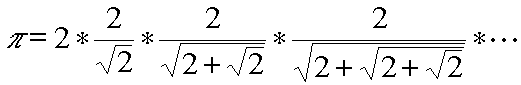
nota:
Le passage de cos(p /2n) à cos(p /2n+1) se fait grâce à la formule : cos(2a) = 2cos²(a)-1
|
|
|
|
|
....... |
........ |
|