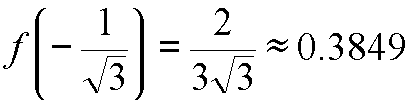![[Graphics:tpd1gr9.gif]](tpd1gr9.gif)
Pivotons cette droite autour du maximum nous remarquons qu'un autre point d'intersection apparaît :
![[Graphics:secante]](tpd1gr15.gif) |
![[Graphics:secante animée]](cubic.gif) |
Problème
: la recherche du maximum d'une fonctionSoit la fonction f définie par f(x) = x3 - x
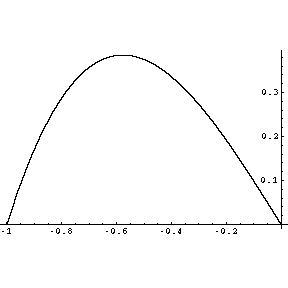
Voici son graphe sur [-1,0]
Nous remarquons qu'elle atteint son maximum
pour une valeur comprise entre -0.6 et -0.5 .
Quelle est cette valeur ?
Caractérisation du maximum
Soit x0 l'abscisse du point où f atteint son maximum.
Traçons la droite horizontale passant par ce point :
![[Graphics:tpd1gr9.gif]](tpd1gr9.gif)
![[Graphics:secante]](tpd1gr15.gif) |
![[Graphics:secante animée]](cubic.gif) |
Ceci nous montre que la tangente horizontale caractérise le maximum.
Dans la suite, nous déterminons l'abscisse du point dont la tangente est horizontale.
Cherchons la pente d'une droite passant par le point (x0,f(x0)) et (x0 + h ,f(x0 + h)).
Cette pente vaut : 3(x0)2 - 1+h ( 3x0 +h).
C'est le calcul de la pente d'une droite passant par deux points.
On obtient la pente de la droite tangente en (x0,f(x0)) pour les deux points très proches,
c'est à dire h très petit. Elle est donnée par :
p = 3(x0)2 - 1.
En particulier, la droite horizontale de pente 0 est donnée par p=0.
Ce qui est équivalent à
3(x0)2 - 1=0
Les solutions de cette équation sont :
![]()
La valeur de x0 est donc
![]() ,
,
la valeur positive ne convient pas car on étudie la fonction pour x entre -1 et 0.
Le maximum vaut