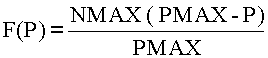
Le but du problème en 1ère ou terminale ES est à la fois d’étudier une modélisation simpliste d’un problème d’économie et de mettre en œuvre les différentes techniques du programme de mathématiques :
Description
Il s'agit de produire des CD-Rom et on cherche à fixer le prix de vente permettant de réaliser le maximum de profits.
I. Prix de revient
On note INV l'investissement et UNI le coût de production d'un CD-Rom. On suppose que la production est de N unités.
Le prix de revient est donc :
REV= INV +N*UNI
II. Loi de l’offre et de la demande
On admet que, plus le prix est bas, plus on vend de CD-Rom et inversement, plus le prix est élevé moins on en vend. Ce constat est modéliser de la façon suivante :
Le modèle
On suppose qu'il y a deux limites : un prix de vente maximum PMAX, que personne ne veut dépasser et une production maximum NMAX (imposée par le marché par exemple).
Soit F une fonction donnant le nombre de ventes en fonction du prix P,
N=F(P).
Exemples de modèle :
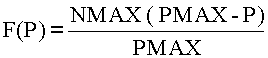
ou
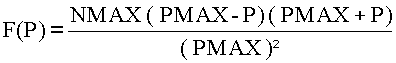
Exemples numériques
NMAX=1 000 000, PMAX=30 Euros.
|
|
|
|
|
|
On remarque que F(0)=NMAX et F(PMAX)=0
III. Bénéfice
Dans cette société on recherche le bénéfice maximum.
Rappel d’école primaire :
bénéfice = prix de vente – prix de revient
BEN= N*P - REV
Remarque
Notons que BEN est une fonction de P car N est une fonction de P et REV une fonction de N.
Par exemple, si N est un polynôme de degré 2 alors BEN est de degré 3.
IV. Exemple de problème
Trouver REV sachant que INV=10 000 et UNI=9.
Chercher la formule du bénéfice en fonction de P pour 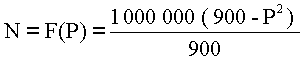 .
.
Pour quelle valeur de P le bénéfice est maximum ?
Combien de CDRom sont vendus ?
Corrigé de l'exercice Corrigé de l'exercice avec le logiciel derive