Linéarité
L1 : (u + v)’ = u’ + v’
L2 : (ku)’ = ku’
La première de ces propriétés, qui peut s’énoncer ainsi :
" la dérivée d’une somme de deux termes est égale à la somme des dérivées "
s’établit en observant que :

l’existence de u’(a) et v’(a), supposée ici, entraîne celle de (u + v)’(a), la valeur de ce nombre dérivé étant u’(a) + v’(a)
(limite du premier quotient + limite du deuxième quotient)
Remarques :
- En combinant L1 et L2 avec k = -1, on obtient : (u - v)’ = u’ - v’
" la dérivée d’une différence est égale à la différence des dérivées "
Pour dériver une somme de plus de deux termes on utilise L1 plusieurs fois ; on retiendra que : " la dérivée d’une somme est égale à la somme des dérivées "
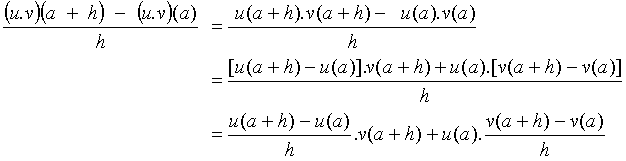



 quand h tend vers 0.
quand h tend vers 0.

 alors f est (strictement) croissante sur I.
alors f est (strictement) croissante sur I. alors f est (strictement) décroissante sur I.
alors f est (strictement) décroissante sur I.