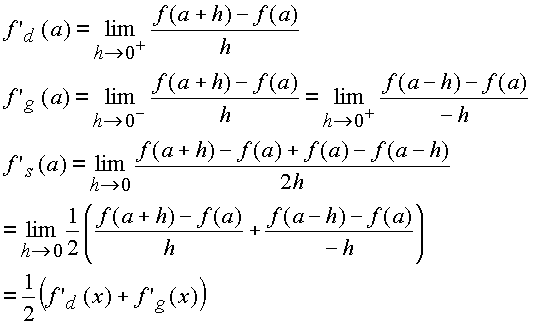une fonction à valeurs réelles de la variable x.La fonction f est dite dérivable en a si le rapport
admet une limite (finie) quand x tend vers
a. Cette valeur, notée f'(a), constitue la
dérivée de f en a ou encore nombre dérivé de
f en a.Introduction: notion de vitesse instantanée.
Soit une fonction à valeurs réelles de la variable x.
La fonction f est dite dérivable en a si le rapport
admet une limite (finie) quand x tend vers
a. Cette valeur, notée f'(a), constitue la
dérivée de f en a ou encore nombre dérivé de
f en a.
La fonction de la variable x dont la valeur pour tout a est égale à la dérivée f'(a) en a de la fonction f est la fonction dérivée de la fonction f. On la note f'.
En posant x = a + h, on a 
.
La dérivée symétrique au point a d'une fonction est
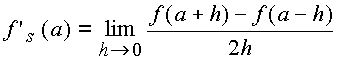
géométriquement, il s'agit de tracer passant les points de la courbe d'abscisses symétrique par rapport à l'abscisse a.
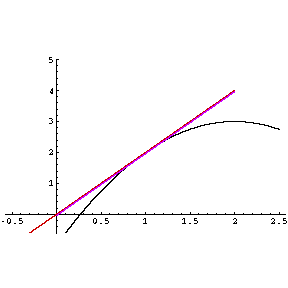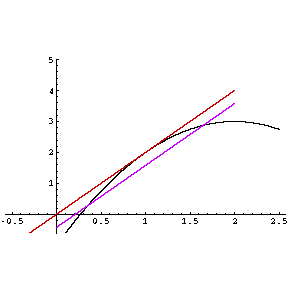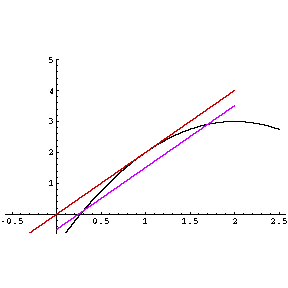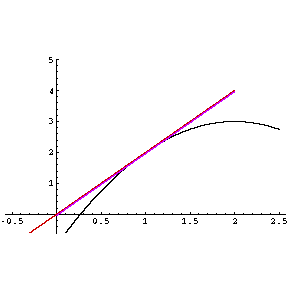
Remarque. Si f est dérivable, elle admet une dérivée symétrique.
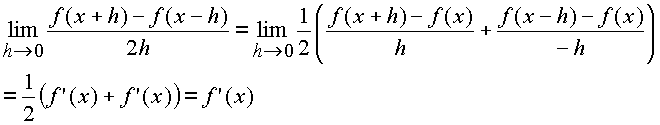
Remarque. Une fonction peut aussi avoir une dérivée symétrique sans qu'elle soit dérivable.
Exemple. Soit f(x)=|x|
Calcul de sa dérivée symétrique en 0.
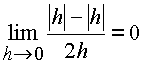
Propriété. Si une fonction admet une dérivée à droite et une dérivée à gauche, alors elle admet une dérivée symétrique.
