|
Introduction Ensemble de définition |
Courbe représentative Sens de Variation |
Pour certains humains, la qualité du sommeil est fonction de la phase de la lune, celle-ci déterminant également la qualité des légumes à venir. Si l’on gratte un peu, on s’aperçoit que pour les uns, la pleine lune serait favorable, alors que ce serait le contraire pour d’autres.
En mathématiques, une fonction est le plus communément donnée par une règle de calcul associant à un nombre (voir plusieurs…) appelé variable, souvent noté x, une image obtenue en appliquant les règles de calcul définissant la fonction.
Exemples :
définit une fonction affine
(l’image du nombre 1 est le nombre 5 (2 ´ 1 + 3)
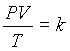permet d’exprimer, pour un gaz parfait donné, donc une constante
k donnée, la pression P en fonction de la température T et du
volume V : 
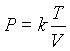. La
règle s’écrit dans ce cas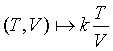 
Si dans le domaine des sciences expérimentales les valeurs possibles des variables sont imposées par leur nature (T, V, P sont des réels positifs…dans l’exemple ci-dessus), en mathématiques, on doit préciser quel est l’ensemble dans lequel la variable x prend ses valeurs : il s’agit de l’ensemble de départ de la fonction. Suivant le choix de cet ensemble de départ, les propriétés de la fonction peuvent s’avérer très différentes.
Exemple : la règle 
,
suivant que x prend toute valeur entière, réelle ou complexe définit une suite
arithmétique, une droite du plan ou une homothétie.
E est l’ensemble de départ, F
l’ensemble d’arrivée
ou plus simplement 
en sous-entendant que E = R
Une fonction f étant donnée, il se peut que pour certaines valeurs de x, élément de l’ensemble de départ, le calcul de l’image f(x) ne soit pas possible.
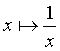n’attribue pas d’image
au réel 0. La fonction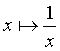 
n’est pas définie en 0.
Définition :
L’ensemble de définition d’une fonction est formé des
éléments de l’ensemble de départ pour lesquels le calcul de l’image est
possible.
Comment déterminer l’ensemble de définition d’une fonction ?
On "analyse" l’expression de f(x).
En présence de quotients, on recherche les valeurs éventuelles de la variable, qui annulent le diviseur.
Ces valeurs ne font pas partie de l’ensemble de définition.
Attention ! L’existence d’un quotient est parfois "cachée" : voir la fonction tangente…
En présence de radicaux, on recherche la ou les valeur(s) éventuelle(s) de la variable, pour lesquelles le radicande est négatif.
Ces valeurs ne font pas partie de l’ensemble de définition.
En présence de la fonction logarithme népérien, ln, on recherche les valeurs éventuelles de la variable, pour lesquelles l’expression sur laquelle ln est appliquée est négative ou nulle.
Ces valeurs ne font pas partie de l’ensemble de définition.
Un repère du plan étant choisi, l’ensemble des points de coordonnées (x ; f(x)) constitue la courbe représentative de f associé à ce repère.
Certaines propriétés (symétrie, périodicité) de la courbe d’une fonction, décelables au niveau de l’expression de la fonction, peuvent être exploitées pour limiter son étude à un ensemble plus restreint que celui de départ, donné à priori.
Symétrie par rapport à l’axe des ordonnées, fonction paire
Si l’ensemble de départ E est symétrique par rapport à 0 et f(-x)
= f(x) pour tout x dans E,
on peut prendre E inter [0 ; +¥ [
comme ensemble d’étude f est dite paire dans ce cas.
On complétera ensuite en utilisant la symétrie par rapport à l’axe des ordonnées.
Symétrie par rapport à l’origine, fonction impaire
Si l’ensemble de départ E est symétrique par rapport à 0 et f(-x)
= -f(x) pour tout x dans E,
on peut prendre E inter [0 ; +¥ [
comme ensemble d’étude f est dite impaire dans ce cas.
On complétera ensuite en utilisant la symétrie par rapport à origine du repère.
Courbe s’obtenant en raccordant des portions de courbes identiques, fonction périodique
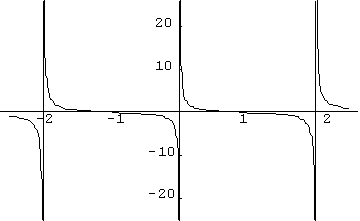Ce tracé correspond à la fonction
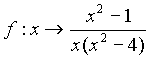
N’est-on pas tenté d’affirmer que f est périodique ?
Motivation : problèmes d’optimisation.
Avec une calculatrice graphique, il est facile aujourd’hui de
visualiser le graphique d’une fonction (ou plus exactement la partie de son graphique
correspondant à une fenêtre de visualisation par défaut ou choisie). Il est tentant
alors d’en " déduire " le sens de variation, i.e. de voir sur
quels intervalles la fonction est croissante (sa courbe va vers le haut) ou décroissante
(la courbe va vers le bas). Il suffit d’observer les situations suivantes pour se
convaincre de la nécessité de bien définir ces notions :
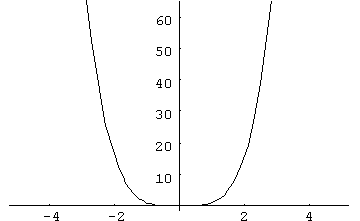
Voici les courbes de 
et 
dans des fenêtres "standard"
 |
 |
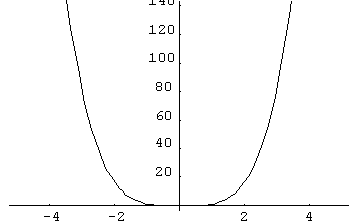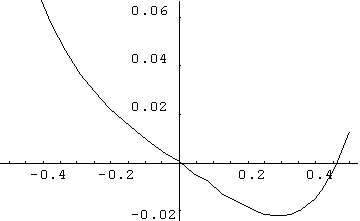
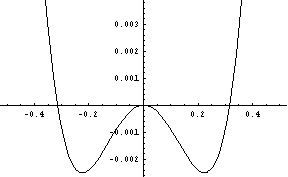
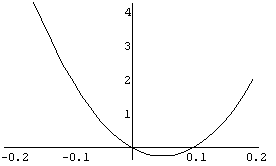
Et dans des fenêtres plus resserrées autour de l’origine
 |
 |
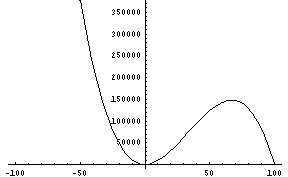
Les courbes suivantes correspondent à la fonction 
dans diverses fenêtres :
| fenêtre "standard" | "zoom" autour de l’origine | |
 |
 |
 |
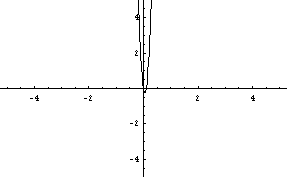Fonction croissante sur un intervalle I :
La fonction f est dite croissante sur I si les images de deux réels quelconques dans I sont rangées dans le même ordre que les réels de départ.
Fonction décroissante sur un intervalle I :
La fonction f est dite décroissante sur I si les images de deux réels quelconques dans I sont rangées dans l’ordre inverse que les réels de départ.
Fonction constante sur un intervalle I :
La fonction f est dite constante sur I si toutes les
images de réels de I sont égales.
f(x) – f(y) = ax + b – (ay + b) = a(x – y)
(i.e. trouver les intervalles sur lesquels la fonction est croissante
ou décroissante)
En théorie, il s’agit de déterminer le signe du rapport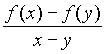 
où x et y
désignent des réels distincts pris dans l’ensemble de définition de f.
En pratique, on utilise souvent le
théorème du signe de la dérivée
Mais il est parfois plus rapide, voire plus élégant d’utiliser
l’un des théorèmes suivants :
La composée de deux fonctions croissantes est croissante
La composée de deux fonctions décroissantes est croissante
La composée d’une fonction croissante et d’une fonction décroissante est décroissante
Exemple : soit la fonction f définie sur R par 
.
et h(x) = 1 – x, on a : f(x) = ln(g(h(x)))